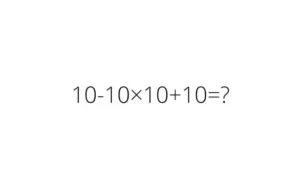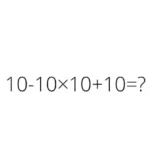Reclamă
Internetul a fost recent cuprins de o provocare matematică pentru gimnaziu care, la prima vedere, pare simplă: „6÷2(1+2) = ?”. Însă aceasta a generat numeroase controverse, cu persoane argumentând pentru rezultate diferite.
Provocarea, aparent simplă, cu ecuația „6÷2(1+2) = ?” a devenit virală pe internet. Deși pare o problemă simplă de matematică, a aprins dezbateri intense, cu participanți care aduc argumente în favoarea unor răspunsuri diferite.
Reclamă
Două variante principale de răspuns au fost propuse. O parte dintre internauți susțin că rezultatul este 1, argumentând că trebuie să se calculeze prima dată paranteza și înmulțirea adiacentă, ceea ce ar rezulta în 6÷2(3) = 6:6 = 1. Alții susțin că răspunsul corect este 9, argumentând că trebuie să calculăm mai întâi paranteza, iar apoi operațiunile se execută de la stânga la dreapta, adică 6÷2·3 = 3·3 = 9.
Regulile matematice standard, cunoscute sub acronimul PEMDAS, care reprezintă ordinea de efectuare a operațiunilor – Paranteze, Exponențiali, Înmulțire/Împărțire, Adunare/Scădere, confirmă că răspunsul corect este 9. Prin aplicarea acestor reguli, se calculează mai întâi operațiunea din paranteză (1+2=3), apoi se efectuează împărțirea (6÷2=3) și, în final, rezultatul se înmulțește cu rezultatul operației din paranteză (3·3=9).
Confuzia a fost generată, probabil, de diferite interpretări ale ordinii operațiilor sau de simbolurile utilizate pentru împărțire și înmulțire. În plus, o regulă istorică anterioară anului 1917 sugerează că ordinea operațiilor era diferită, ceea ce duce la un răspuns de 1. Această metodă, însă, nu mai este predată în majoritatea școlilor de astăzi.
Situația demonstrează importanța clarității în matematică și cât de ușor pot apărea dispute pe tema interpretării unei simple expresii matematice. Soluția ar fi înțelegerea și aplicarea corectă a regulilor matematice, asigurându-se că expresiile matematice sunt cât mai clare și neambigue.
Citeste si
- 1. Anunț despre PUNCTUL DE PENSIE! Este răsturnare totală de situație. SURPRIZă pentru toți pensionarii din România r
- 2. Profeții îngrozitoare! Nostradamus și Baba Vanga pentru 2025: Război devastator în Europa